Plot line of sight diagnostics

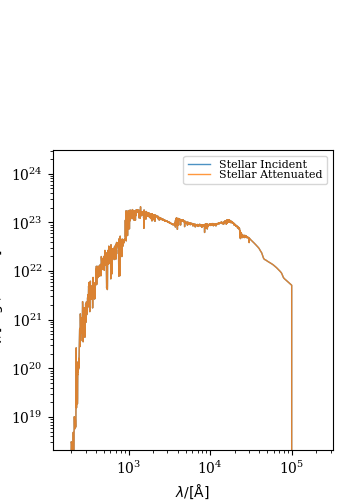
This example shows how to compute line of sight dust surface densities, and plots some diagnostics.

(<Figure size 350x500 with 1 Axes>, <Axes: xlabel='$\\lambda/[\\mathrm{\\AA}]$', ylabel='$L_{\\nu}/[\\mathrm{\\rm{erg} \\ / \\ \\rm{Hz \\cdot \\rm{s}}}]$'>)

import time

import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial import cKDTree
from unyt import Mpc, Msun, Myr

from synthesizer.emission_models import TotalEmission
from synthesizer.emission_models.attenuation import PowerLaw
from synthesizer.grid import Grid
from synthesizer.kernel_functions import Kernel
from synthesizer.parametric import SFH, ZDist
from synthesizer.parametric import Stars as ParametricStars
from synthesizer.particle.galaxy import Galaxy
from synthesizer.particle.gas import Gas
from synthesizer.particle.particles import CoordinateGenerator
from synthesizer.particle.stars import sample_sfzh

plt.rcParams["font.family"] = "DeJavu Serif"
plt.rcParams["font.serif"] = ["Times New Roman"]


def calculate_smoothing_lengths(positions, num_neighbors=56):
    """Calculate the SPH smoothing lengths for a set of coordinates."""
    tree = cKDTree(positions)
    distances, _ = tree.query(positions, k=num_neighbors + 1)

    # The k-th nearest neighbor distance (k = num_neighbors)
    kth_distances = distances[:, num_neighbors]

    # Set the smoothing length to the k-th nearest neighbor
    # distance divided by 2.0
    smoothing_lengths = kth_distances / 2.0

    return smoothing_lengths


# Set the seed
np.random.seed(42)

start = time.time()

# Get the location of this script, __file__ is the absolute path of this
# script, however we just want to directory
# script_path = os.path.abspath(os.path.dirname(__file__))

# Define the grid
grid_name = "test_grid"
grid_dir = "../../tests/test_grid/"
grid = Grid(grid_name, grid_dir=grid_dir)

# Define the model
model = TotalEmission(
    grid,
    tau_v="tau_v",
    dust_curve=PowerLaw(slope=-1),
    fesc=0.1,
    per_particle=True,
)

# Define the grid (normally this would be defined by an SPS grid)
log10ages = np.arange(6.0, 10.5, 0.1)
metallicities = 10 ** np.arange(-5.0, -1.5, 0.1)
Z_p = {"metallicity": 0.01}
metal_dist = ZDist.DeltaConstant(**Z_p)
sfh_p = {"duration": 100 * Myr}
sfh = SFH.Constant(**sfh_p)  # constant star formation

# Generate the star formation metallicity history
mass = 10**10 * Msun
param_stars = ParametricStars(
    log10ages,
    metallicities,
    sf_hist=sfh,
    metal_dist=metal_dist,
    initial_mass=mass,
)

# How many stars and gas particles?
nstars = 1000
ngas = 1000

# Generate some random coordinates
coords = CoordinateGenerator.generate_3D_gaussian(nstars)

# Calculate smoothing lengths
smls = calculate_smoothing_lengths(coords)

# Sample the SFZH, producing a Stars object
# we will also pass some keyword arguments for attributes
# we will need for imaging
stars = sample_sfzh(
    param_stars.sfzh,
    param_stars.log10ages,
    param_stars.log10metallicities,
    nstars,
    coordinates=coords * Mpc,
    current_masses=np.full(nstars, 10**8.7 / nstars) * Msun,
    smoothing_lengths=smls * Mpc,
    redshift=1,
)

# Now make the gas

# Generate some random coordinates
coords = CoordinateGenerator.generate_3D_gaussian(ngas)

# Calculate the smoothing lengths
smls = calculate_smoothing_lengths(coords)

gas = Gas(
    masses=np.random.uniform(10**6, 10**6.5, ngas) * Msun,
    metallicities=np.random.uniform(0.01, 0.05, ngas),
    coordinates=coords * Mpc,
    smoothing_lengths=smls * Mpc,
    dust_to_metal_ratio=0.2,
)

# Create galaxy object
galaxy = Galaxy("Galaxy", stars=stars, gas=gas, redshift=1)


# Get the SPH kernel
sph_kernel = Kernel()
kernel_data = sph_kernel.get_kernel()

# Calculate the tau_vs
galaxy.get_stellar_los_tau_v(
    kappa=0.07,
    kernel=kernel_data,
    force_loop=False,
)

# Get the spectra (this will automatically use the tau_vs we just calculated
# since the emission model has tau_v="tau_v")
galaxy.stars.get_spectra(model)

# Integrate the particle spectra
galaxy.integrate_particle_spectra()

# Plot the Sed
galaxy.plot_spectra(show=True, combined_spectra=False, stellar_spectra=True)