Rotating particle distributions

This example demonstrates how to rotate a particle distribution and a galaxy.

This example uses a completely fake example of a galaxy with a disk and bulge component. We generate some coordinates for the disk and bulge, and then generate some velocities for the disk and bulge.

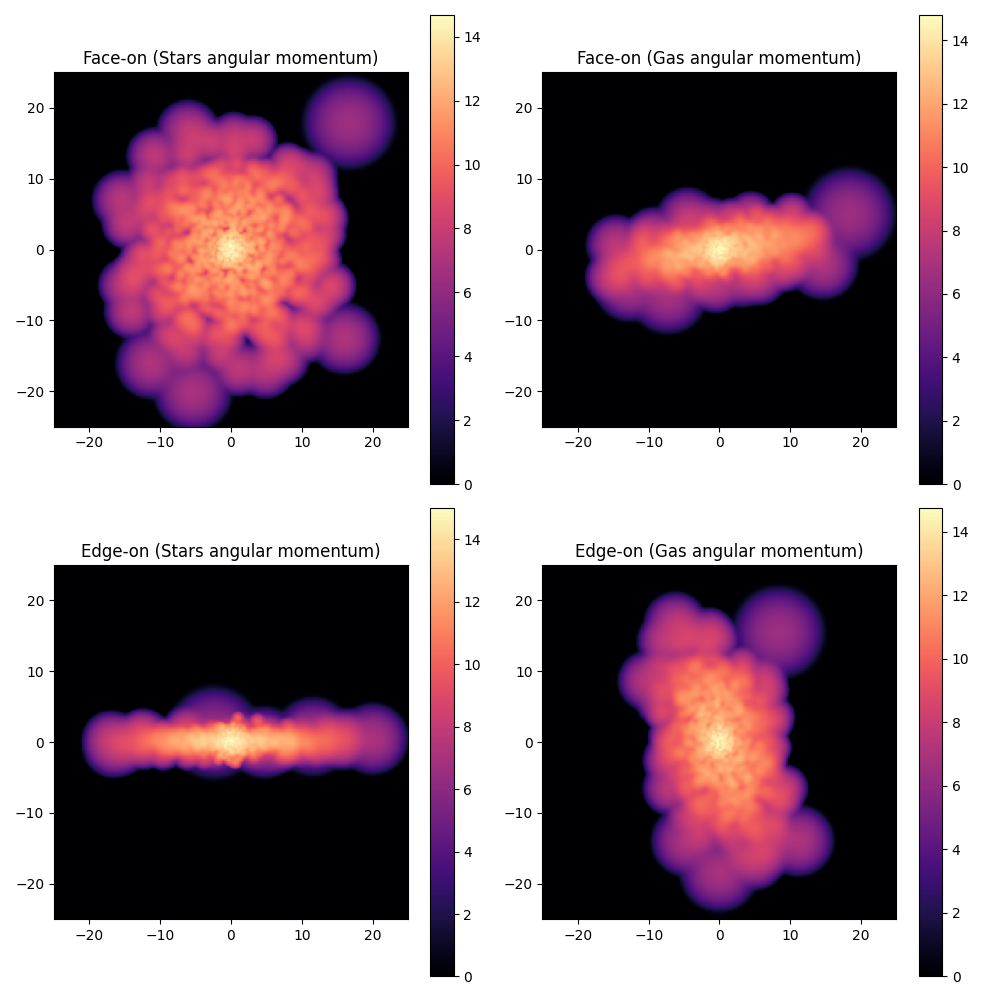
We demonstrate the different ways to rotate a particle distribution and a galaxy. Finally showing an image of the face-on and edge-on views of the galaxy.

Angular momentum before rotation: [-1.00567885e+26 -2.20430946e+25  4.19491538e+28] Msun*km**2/s
Rotating stars by phi=269.3947684040967 degree, theta=156.37630149658568 degree
Angular momentum after rotation: [ 1.68294228e+28  1.00795118e+26 -3.84252843e+28] Msun*km**2/s
Angular momentum of face-on stars: [ 2.13735988e+13  1.07766045e+11 -4.19492802e+28] Msun*km**2/s
Angular momentum of edge-on stars: [4.19492802e+28 1.08664095e+11 2.13771910e+13] Msun*km**2/s
Rotating galaxy by phi=245.64543353442713 degree, theta=23.225201431032307 degree

import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial import cKDTree
from unyt import Msun, Myr, degree, km, kpc, s

from synthesizer.kernel_functions import Kernel
from synthesizer.particle import CoordinateGenerator, Galaxy, Gas, Stars


def calculate_smoothing_lengths(positions, num_neighbors=56):
    """Calculate the SPH smoothing lengths for a set of coordinates."""
    tree = cKDTree(positions)
    distances, _ = tree.query(positions, k=num_neighbors + 1)

    # The k-th nearest neighbor distance (k = num_neighbors)
    kth_distances = distances[:, num_neighbors]

    # Set the smoothing length to the k-th nearest neighbor
    # distance divided by 2.0
    smoothing_lengths = kth_distances / 2.0

    return smoothing_lengths


# Set the seed
np.random.seed(42)

# First define the covariance matrices for a disk and bulge component
# of a galaxy. We'll use this as a fake example.
disk_cov = np.array(
    [
        [30.0, 0, 0],  # Larger spread in x direction
        [0, 30.0, 0],  # Larger spread in y direction
        [0, 0, 0.5],  # Smaller spread in z direction (flattened)
    ]
)
bulge_cov = np.array(
    [[1.0, 0, 0], [0, 1.0, 0], [0, 0, 1.0]]  # Equal spread in all directions
)

# Now we'll generate some coordinates for the disk and bulge
n_disk = 1000
n_bulge = 500
disk_coords = CoordinateGenerator.generate_3D_gaussian(n_disk, cov=disk_cov)
bulge_coords = CoordinateGenerator.generate_3D_gaussian(n_bulge, cov=bulge_cov)
coords = np.vstack([disk_coords, bulge_coords]) * kpc

# We'll also need to generate some velocities for the disk and bulge. The bulge
# will be in a random direction, while the disk will be in the x-y plane.
vrot = 200  # Circular rotation speed in the disk
sigma_bulge = 50  # Velocity dispersion for bulge particles
disk_velocities = np.zeros((n_disk, 3))
angles = np.arctan2(disk_coords[:, 1], disk_coords[:, 0])
disk_velocities[:, 0] = -vrot * np.sin(angles)  # Tangential velocity in x
disk_velocities[:, 1] = vrot * np.cos(angles)  # Tangential velocity in y
bulge_velocities = np.random.normal(0, sigma_bulge, size=(n_bulge, 3))
velocities = np.vstack([disk_velocities, bulge_velocities]) * km / s


# Define the other properties we'll need
masses = np.ones(n_disk + n_bulge) * 1e6 * Msun
ages = np.random.rand(n_disk + n_bulge) * 100 * Myr
metallicities = np.random.rand(n_disk + n_bulge) * 0.02
initial_masses = masses.copy()
redshift = 0.0
centre = np.array([0.0, 0.0, 0.0]) * kpc
smoothing_lengths = calculate_smoothing_lengths(coords) * kpc

# We'll start by simply using some stars
stars = Stars(
    initial_masses,
    ages,
    metallicities,
    coordinates=coords,
    current_masses=masses,
    velocities=velocities,
    redshift=redshift,
    centre=centre,
    smoothing_lengths=smoothing_lengths,
)

print(f"Angular momentum before rotation: {stars.angular_momentum}")

# We can rotate any particle based object (or a galaxy) by any phi and theta
# (these must be passed with units)
phi = np.random.rand() * 360 * degree
theta = np.random.rand() * 180 * degree
print(f"Rotating stars by phi={phi}, theta={theta}")
stars.rotate_particles(phi=phi, theta=theta, inplace=True)

# So we can simply make images we'll attach these stars to a galaxy
galaxy = Galaxy(stars=stars)

print(f"Angular momentum after rotation: {galaxy.stars.angular_momentum}")

# You can also rotate to face-on and edge-on, here we will also leave the
# original stars unchanged and get a new stars object with the rotations
# applied
face_on_stars = stars.rotate_face_on(inplace=False)
edge_on_stars = stars.rotate_edge_on(inplace=False)

# Make a galaxy to generate the images
face_on_galaxy = Galaxy(stars=face_on_stars)
edge_on_galaxy = Galaxy(stars=edge_on_stars)

# Print the angular momentum of the face-on and edge-on stars
print(
    "Angular momentum of face-on stars: "
    f"{face_on_galaxy.stars.angular_momentum}"
)
print(
    "Angular momentum of edge-on stars: "
    f"{edge_on_galaxy.stars.angular_momentum}"
)

# As well as rotating at the component level you can rotate an entire
# galaxy. This will rotate all attached components. First we need a galaxy so
# lets add some gas too.
ngas = 2000
gas_cov = np.array(
    [
        [10.0, 0, 0],  # Larger spread in x direction
        [0, 20.0, 0],  # Larger spread in y direction
        [0, 0, 30.0],  # Larger spread in z direction
    ]
)
gas_coords = CoordinateGenerator.generate_3D_gaussian(ngas, cov=gas_cov) * kpc
gas_velocities = np.random.normal(0, 50, size=(ngas, 3)) * km / s
gas_masses = np.ones(ngas) * 1e6 * Msun
gas_metallcities = np.random.rand(ngas) * 0.02
gas = Gas(
    gas_masses,
    coordinates=gas_coords,
    velocities=gas_velocities,
    metallicities=gas_metallcities,
    redshift=redshift,
    centre=centre,
    dust_to_metal_ratio=0.3,
    smoothing_lengths=calculate_smoothing_lengths(gas_coords) * kpc,
)

# Make the galaxy
galaxy = Galaxy(stars=stars, gas=gas, redshift=redshift, centre=centre)

# As before we can pass phi and theta to rotate the entire galaxy (for all the
# following examples we'll do every inplace)
phi = np.random.rand() * 360 * degree
theta = np.random.rand() * 180 * degree
print(f"Rotating galaxy by phi={phi}, theta={theta}")
galaxy.rotate_particles(phi=phi, theta=theta, inplace=True)

# We also have the face on and edge on helpers but for the entire galaxy we
# need to specify which component we want to use as the reference for the
# rotation. By default this will use the stars component. Below we show
# how to do this and make some images of the stellar distribution rotated
# to align with both the stars and gas component's angular momentum.

# First we'll rotate the galaxy to face-on using the stars component
galaxy.rotate_face_on(inplace=True, component="stars")

# Make the image
face_on_stars_img = galaxy.get_map_stellar_mass(
    resolution=0.1 * kpc,
    fov=50 * kpc,
    img_type="smoothed",
    kernel=Kernel().get_kernel(),
)
face_on_stars_img.arr = np.arcsinh(face_on_stars_img.arr)

# Rotate the gas to be face on
galaxy.rotate_face_on(inplace=True, component="gas")

# Make the image
face_on_gas_img = galaxy.get_map_stellar_mass(
    resolution=0.1 * kpc,
    fov=50 * kpc,
    img_type="smoothed",
    kernel=Kernel().get_kernel(),
)
face_on_gas_img.arr = np.arcsinh(face_on_gas_img.arr)

# Rotate the stars to be edge on
galaxy.rotate_edge_on(inplace=True, component="stars")

# Make the image
edge_on_stars_img = galaxy.get_map_stellar_mass(
    resolution=0.1 * kpc,
    fov=50 * kpc,
    img_type="smoothed",
    kernel=Kernel().get_kernel(),
)
edge_on_stars_img.arr = np.arcsinh(edge_on_stars_img.arr)

# Rotate the gas to be edge on
galaxy.rotate_edge_on(inplace=True, component="gas")

# Make the image
edge_on_gas_img = galaxy.get_map_stellar_mass(
    resolution=0.1 * kpc,
    fov=50 * kpc,
    img_type="smoothed",
    kernel=Kernel().get_kernel(),
)
edge_on_gas_img.arr = np.arcsinh(edge_on_gas_img.arr)

# Plot the images
fig, axes = plt.subplots(2, 2, figsize=(10, 10))
face_on_stars_img.plot_map(
    fig=fig,
    ax=axes[0, 0],
    show=False,
    extent=(-25, 25, -25, 25),
    cmap="magma",
)
axes[0, 0].set_title("Face-on (Stars angular momentum)")
face_on_gas_img.plot_map(
    fig=fig,
    ax=axes[0, 1],
    show=False,
    extent=(-25, 25, -25, 25),
    cmap="magma",
)
axes[0, 1].set_title("Face-on (Gas angular momentum)")
edge_on_stars_img.plot_map(
    fig=fig,
    ax=axes[1, 0],
    show=False,
    extent=(-25, 25, -25, 25),
    cmap="magma",
)
axes[1, 0].set_title("Edge-on (Stars angular momentum)")
edge_on_gas_img.plot_map(
    fig=fig,
    ax=axes[1, 1],
    show=False,
    extent=(-25, 25, -25, 25),
    cmap="magma",
)
axes[1, 1].set_title("Edge-on (Gas angular momentum)")
plt.tight_layout()
plt.show()